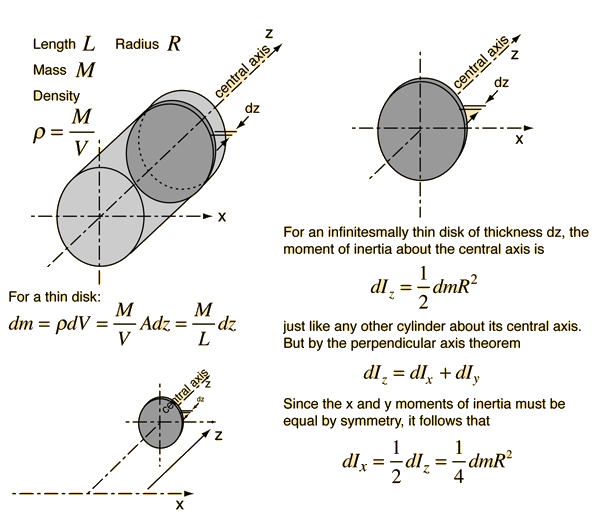Second Moment Of Inertia For Solid Cylinder

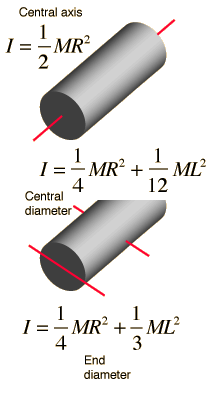
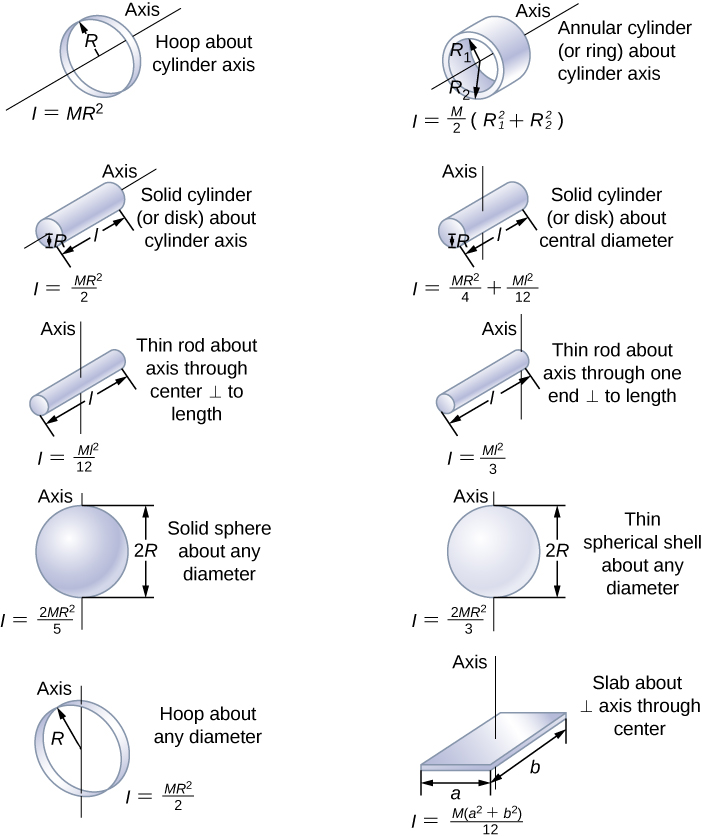
I 1 2 m r 2.

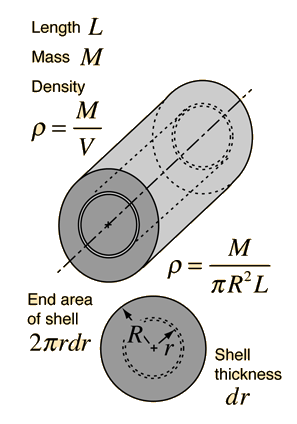
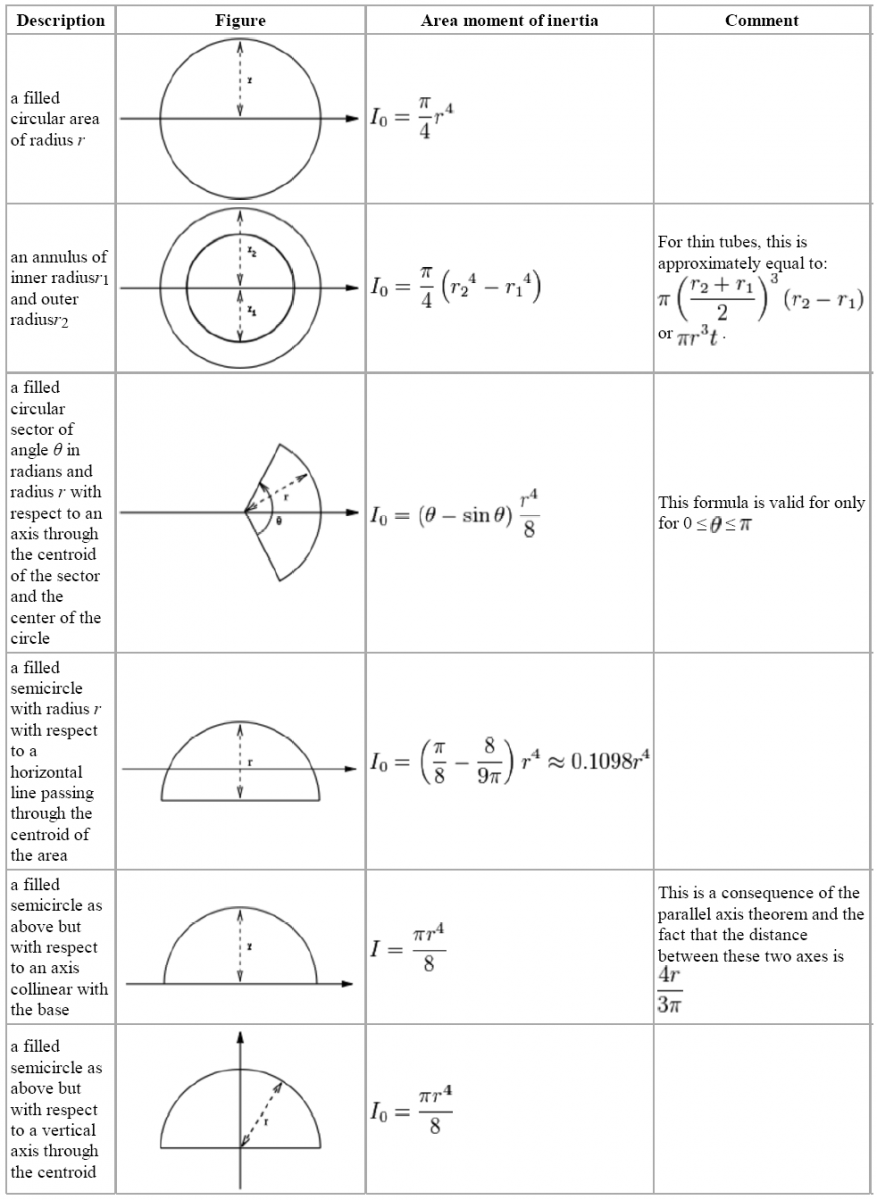
Second moment of inertia for solid cylinder. The second moment of area also known as area moment of inertia is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. This involves an integral from z 0 to z l. Moreover in order to obtain the moment of inertia for a thin cylindrical shell otherwise known as a hoop we can substitute r 1 r 2 r as the shell has a negligible thickness. The unit of dimension of the second moment of area is length to fourth power l 4 and should not be confused with the mass moment of inertia.

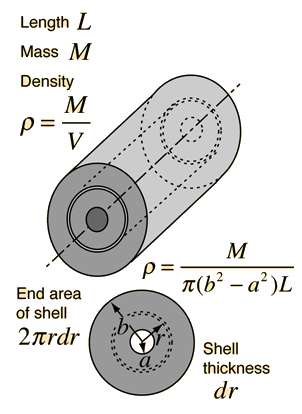
If the piece is thin however the mass moment of inertia equals the area density times the area moment of inertia. Obtaining the moment of inertia of the full cylinder about a diameter at its end involves summing over an infinite number of thin disks at different distances from that axis. Moment of inertia of a solid cylinder. To understand the full derivation of the equation for solid cylinder students can follow the interlink.

I frac 1 2 mr 2 i 21. Here m total mass and r radius of the cylinder. A solid cylinder s moment of inertia can be determined using the following formula. Moment of inertia of a solid cylinder about its centre can be found using the following equation or formula.

For any given disk at distance z from the x axis using the parallel axis theorem gives the moment of inertia about the x axis.